Save 90% of energy lost, continuous exterior rigid insulation
Step by step calculation on energy savings for a exterior rigid insulation. One change to approaching insulation; 92% saving from energy lost
The Monk
6/30/20244 min read
Well there is a lot of hype on continuous rigid insulation in the rest of the world. Even Australian Depart of Energy wishes that it can bring it into the standards, but fell short of it.
It's hard to go against the industry even if it is at the best interest of people you see..
Reference from Youhome.gov.au website below
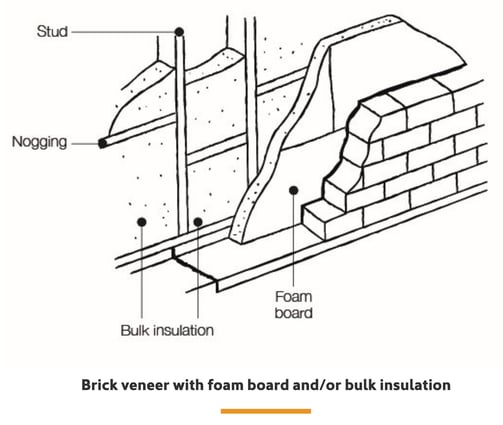
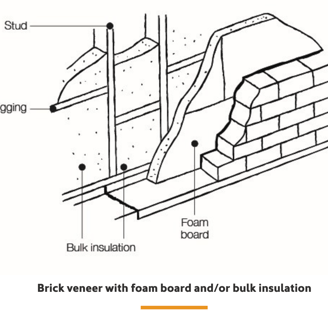
Fixing insulation to the outside of the studs helps reduce thermal bridging in cold climates. Suitable materials include PIR and PUR or XPS boards, or foil-faced boards with a reflective surface and air space of at least 25mm. Placing the insulation on the outside of the wall frame gives a higher total R value than placing the insulation between the studs. Leave sufficient space for bricklayers to lay the outside skin (about 40mm), and keep in mind that brick cavity ties need to be installed, typically through sheet joints.
In this post I am going to describe how to calculate the energy savings that we can achieve by just by approaching the design aspect of insulation.
From traditional age old approach to insulation using a the Batts between frame to an exterior rigid insulation -- the approach that allows insulation to be continuous. If you are new to the concept of exterior insulation, I suggest you catch up on the concept here.
With that said, lets proceed. In the following section, I am going to take one of projects and explain how we calculate the energy savings,
The project is about 400 sqm double story home in suburban Melbourne. The structural engineer has designed it to be a 90mm timber framed work. Let's calculate the insulation efficiencies here,
A simple formula to calculate the effective R value is,
Where:
R(eff) = Effective R-value of the wall assembly
A(ins) = Fraction of the wall area occupied by insulation
A(frame) = Fraction of the wall area occupied by framing
R(ins) = R-value of the insulation
R(frame) = R-value of the framing
Case 1: Internal insulation - Batt Insulation between timber frames
Stud Wall: 90 mm
Material R-Value of Batt Insulation: Assume R-2.5 per 25 mm, so R-8.82 per 90 mm. This is ideal, in real world, the electricians and plumbers will mess up the insulation all the time, let alone a proper gap free installation.
Framing R-Value: Timber framing typically has an R-value of about R-1.4 per 25mm, or R-5.0 per 90 mm.
Area Occupied by Insulation and Framing: Using the same 16-inch on center framing, which has
Insulation: 14.5/16 = 0.90625 (90.625%)
Framing: 1.5/16 = 0.09375 (9.375%) about 90% of insulation and 10% of frame exposed approx.
Now, knowing this let's substitute the values in the above formula,
R(eff) = ?
A(ins) = 90% or 0.9
A(frame) = 10% or 0.1
R(ins) = R 5 (50 mm Batts of R2.5 per 25 mm)
R(frame) = R 5.5 (R1.4 per 25mm of timber)
The effective RValue using this calculation is
=1/((0.9/5)+(0.1/5.5)) = 5.5.
So, the effective R Value of our timber stud home with Batts insulation is about R5.5.
Notice the overall insulation of the timber is higher than the Batts itself 🤷🏽- #stateofinsulation
Case 2: Continuous Exterior Rigid insulation
The stud thickness doesn't count here because, the insulation pretty much resides outside the frame structure -- that is how we are able to get a continuous coverage of insulation throughout. This also means there is no thermal bridging in this concept -- as long as it is installed properly. There is an element of trade there. A 50mm rigid insulation installed outside the timber frame continuously and taped correctly - has that as the effective insulation value too. However, if there is a brick tie or some other material that is penetrating the insulation layer or if the insulation is not properly taped there is a chance the efficiency will reduce too. But this doesn't present the same risk as the other.
There are two parameters in the calculation,
Based on the rigid insulation material used
The thickness of the insulation.
For the given home, we are settling with a 50mm XPS foam board. The other options are Expanded foam (EPS), Extruded Foam (XPS) or Polyiso. While Polyiso is even better efficient, its expensive, so, we settled with XPS foam board.
Assuming our foam board as having R5 per 25mm - which is very achievable for an XPS foam, for a 50mm foamboard, the RValue corresponds to R10.
The effective RValue of Continuous Exterior Rigid insulation stands at R10.
If we are using the internal insulation as well to compliment the exterior the overall RValue become R10 + effective value of internal insulation, taking us to R18.31 in all.
Energy saving calculation
For the sake of this calculation, we are going to assume on an average there is 10 degrees difference between outside the house and inside the outcome. That is if the temp inside the house is 21 deg celsius the outside temperate is assumed as either 11 deg celsius or 31 deg celsius. This may not be absolutely correct, but keeps the calculation easy. It also tells that on the extreme energy consuming days how much energy we save.
The formula for calculating the energy requirement is,
Total energy required for a 400 sqm
Batt Insulated house is = 400*10/5.5 = 727.27 watts
Continuous rigid insulated house (no batts) = 400*10/10 = 400 watts
Continuous rigid insulated house (with batts) = 400*10/18.31 = 281.5 watts
Assuming the energy saved by better insulation corresponds to the energy saved in heating/cooling the home (bear in mind, this is also approximation -- in real world with the varying temp during day, night and day of the year -- this is never perfect).
Energy saved by Continuous insulation without batts = (727.27-400)*100/481.32 = 68%
Energy saved by continuous insulation with batts = (727.27-281.5)*100/481.35 = 92.6%
We can replace the current insulation standards with a continuous exterior insulation and save 68% of energy lost just like that.
We can compliment the current insulation with continuous exterior insulation and save 92.6% energy lost - that is half the energy lost.
